Inleiding

Voorbeeld 1: 

De behaalde scores in klas A zijn: 5,6,6,6,7,7,7,8.
De behaalde scores in klas B zijn: 2,3,3,5,9,10,10,10.
Als we het gemiddelde berekenen voor klas A en B bekomen we voor beiden 6,5. Alhoewel de gemiddelden gelijk zijn, liggen de scores in klas A veel dichter bij het gemiddelde dan de scores in klas B. M.a.w. de scores in klas B zijn veel meer gespreid. 

Voorbeeld 2:
Een producent in frisdranken brengt twee soorten limonades op de markt. De flessen waarop 1 liter als inhoud vermeld staat, worden automatisch gevuld door twee machines A en B. Bij een controle worden 100 flessen van elk vulmachine op hun inhoud getest. De meetresultaten van de controleproef zijn weergegeven met de volgende staafdiagrammen. 

Beide machines leveren gevulde flessen af met een gemiddelde inhoud van 1 liter. Toch is er een opvallen verschil tussen beide machines: de inhouden van de flessen gevuld door machine A, liggen minder gespreid t.o.v. het gemiddelde en de mediaan, dan de inhouden van de flessen gevuld door machine B. Bijgevolg vult machine A de flessen met frisdrank nauwkeuriger dan machine B!

Voorbeeld 3: 
In het gezin van onze buren is Els 28 jaar, haar man Karel is 32 jaar en hun twee kinderen zijn 3 en 5 jaar. De gemiddelde leeftijd in het gezin is dus 17 jaar. Ook de gemiddelde leeftijd van de leerlingen van de klas waaraan Karel les geeft is 17 jaar! Maar de leeftijden van die leerlingen liggen zonder twijfel meer gegroepeerd rond het gemiddelde dan dit het geval is bij het gezin van Karel en Els. 

Uit deze drie voorbeelden mogen we besluiten dat centrummaten alleen, niet voldoende informatie geven over een reeks data. Om de spreiding van de data uit te drukken, gebruiken we spreidingsmaten. Deze kenmerkende getallen beschrijven hoever de data uit elkaar liggen. We bespreken nu enkele spreidingsmaten. 

1. Variatiebreedte of spreidingsbreedte

De spreidingsbreedte is het verschil tussen het grootte en het kleinste waarnemingsgetal.
Notatie: R (van het Engelse 'range)
Formule: R = xmax- xmin

De spreidingsbreedte van voorbeeld 1 voor de klassen A en B zijn respectievelijk R(A) = 8-5 = 3 en R(B) = 10-2 = 8. De grotere spreidingsbreedte van klas B wijst erop dat de scores veel meer gespreid zijn dan in klas A. Een zeer groot of zeer klein waarnemingsgetal dat sterk afwijkt van de andere data, beïnvloedt sterk de spreidingsbreedte. 

Voor gegroepeerde gegevens geldt: de spreidingsbreedte is het verschil van de bovengrens van de laatste klasse en de ondergrens van de eerste klasse. 

Bij de controle van de massa van 40 blikjes conserven zijn de waarnemingsgetallen gegroepeerd in klassen. Als eerste klasse bekwamen we [485,488[ en als laatste klasse [512,515[ (zie vorige hoofdstukken). Hier is dan R=515-485=30.

2. Interkwartielafstand

Om de spreidingsmaat niet uitsluitend te laten afhangen van het kleinste en het grootste waarnemingsgetal, zoals bij de variatiebreedte, kun jet het eerste en het derde kwartiel als vergelijkingspunten nemen. 

De interkwartielafstand van een reeks gegevens is het verschil van het derde en het eerste kwartiel. Deze afstand wordt bepaald door het interval  [Q1,Q3] dat ongeveer 50% van de middelste waarnemingsgetallen bevat. 

Notatie: Q
Formule: Q=Q3-Q1

Als de interkwartielafstand klein is, dan betekent dit dat de waarnemingsgetallen goed bij de mediaan aansluiten.

4. Boxplot

Uit bovenstaande puntenreeks beschouwen we de volgende vijf kenmerkende maten:

• het kleinste waarnemingsgetal xmin=3;
• het eerste kwartiel Q1=5;
• de mediaan Me=7;
• het derde kwartiel Q3=8;
• het grootste waarnemingsgetal xmax=9.

Deze getallen kunnen we voorstellen op een lijnstuk boven een getallenas. Als we tussen de kwartielen Q1 en Q3 een doos (box) tekenen (plot), dan bekomen we een boxplot, zoals hieronder afgebeeld. 

• De lengte van de boxplot komt overeen met de spreidingsbreedte 6. 
• De uiteinden van de box duiden op de getallenas respectievelijk het eerste kwartiel 5 en het derde kwartiel 8 aan. 
• De lengte van de box komt overeen met de interkwartielafstand 8-5 of 3. 

In de box zitten ongeveer de helft van de data. De andere helft ligt buiten de box tussen de uiteinden van het lijnstuk. 

De boxplot is een handig hulpmiddel om het centrum en de spreiding van verschillende reeksen data in één oogopslag met elkaar te vergelijken.

Teken volgende boxplot na in Excel en upload de file in Smartschool op de voorziene plaats. 

3. Variantie en standaardafwijking

1.      Ruwe gegevens
Je kunt overwegen om de afwijking van elk waarnemingsgetal ten opzichte van het gemiddelde te gebruiken om een norm van spreiding te bepalen. De som van de afwijkingen ten opzichte van het gemiddelde is echter altijd gelijk aan 0. 

Voorbeeld: In de inleiding van dit hoofdstuk zijn de scores weergegeven van 8 leerlingen van een klas A en van een klas B. In beide klassen is het gemiddelde 6,5. We bekijken nu de afwijkingen t.o.v. het gemiddelde:

Om de afwijkingen van alle waarnemingsgetallen t.o.v. het gemiddelde toch te kunnen gebruiken als norm van spreiding, kan men de afwijkingen kwadrateren. 

De variantie van een reeks gegevens is het gemiddelde van de kwadraten van de afwijkingen van de gegevens t.o.v. het gemiddelde. 

De variantie van de populatie mag enkel gebruikt worden wanneer de gegevens de volledige populatie voorstellen. Voor grote waarden van s is het verschil tussen beide varianties echter klein. 

Voorbeeld: 
We berekenen de variantie van de scores van de 8 leerlingen van klas A en klas B. 

Merk op dat de variantie in klas A < de variantie in klas B. Dit duidt er op dat de spreiding van de scores in klas A kleiner is dan in klas B. 

Door het kwadrateren van afwijkingen, zal de variantie uitgedrukt zijn in een andere eenheid dan bij de waarnemingsgetallen. Hebben de waarnemingsgetallen betrekking op lengten, uitgedrukt in cm, dan heeft de variantie de cm² als eenheid. Dit is totaal zinloos. Daarom zullen we een nieuw spreidingsgetal invoeren dat opnieuw uitgedrukt is in dezelfde eenheid als waarnemingsgetallen zelf, namelijk de standaardafwijking of standaarddeviatie. 

De standaardafwijking is de positieve vierkantswortel van de variantie. 

Afspraak: De standaardafwijking noteren we meestal met 2 decimalen meer dan de waarnemingsgetallen. 

Voorbeeld: We berekenen de standaardafwijking van de scores van de 8 leerlingen van klas A en klas B. 

2.     Verwerkte, niet-gegroepeerde gegevens
Als de gegevens verwerkt zijn, kunnen we gebruik maken van de frequenties om de variantie of de standaardafwijking te berekenen.

Voorbeeld: 
We berekenen de standaardafwijking van de scores van 24 leerlingen van een klas. Het gemiddelde was 5,7. 

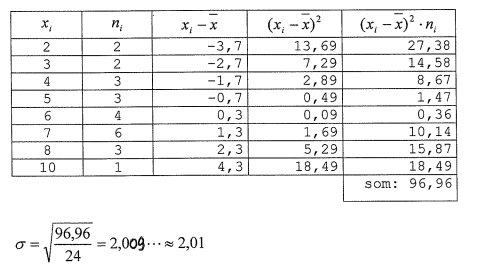
Hoe hebben de leerlingen binnen deze groep gewerkt? 

• De leerlingen die een score behaalden die hoogstens σ afwijkt van het gemiddelde hebben normaal gewerkt. Dit zijn de leerlingen met een score behorend tot [x-σ,x+σ] = [3,69;7,71], of nog, de leerlingen met een score 4, 5, 6 of 7. 
• De leerlingen die een score behaalden die kleiner is dan x-σ hebben minder dan normaal gewerkt. Dit zijn de leerlingen die 3 of minder scoorden. 
• De leerlingen die een score behaalden die groter is dan x+σ hebben meer dan normaal gewerkt. Dit zijn de leerlingen die 8 of meer scoorden. 

3.     Verwerkte, gegroepeerde gegevens
Als de gegevens in klassen werden ingedeeld, kennen we de exacte waarde van de gegevens niet meer. In dat geval zullen we om de variantie of de standaardafwijking te berekenen, elk gegeven vervangen door het klassenmidden van de klasse waartoe dat gegeven behoort. 

Voorbeeld:
We berekenen de standaardafwijking van de massa van 40 blikjes conserven. Als gemiddelde vonden we 499,7. 

Welke blikjes conserven hebben een normale massa? 

• de blikjes conserven waarvan de massa 494g, 495g, ..., 506g is, hebben een 'normale' massa. 
• de blikjes conserven die minder dan 494g wegen, hebben een 'minder dan normale' massa. 
• de blikjes conserven die meer dan 506g wegen, hebben een 'meer dan normale' massa. 

Download onderstaande file, maak de oefeningen en upload deze op de voorziene plaats in Smartschool.